How To Check If A Number Is Prime Or Not C#

You discovered methods to print prime numbers inside a variety and certainly one of several preferred strategies referred to as Sieves of Erastosthenes. You noticed the algorithm, pseudocode, C program, time, and area complexities for every of the strategies that we've discussed. Near the start of the twentieth century, it was proven that a corollary of Fermat's little theorem might possibly be used to check for primality. This resulted within the Pocklington primality test. However, as this take a look at requires a partial factorization of n− 1 the operating time was nonetheless extraordinarily sluggish within the worst case.

Many additional enhancements have been made, however none should be established to have polynomial operating time. In practice, this algorithm is slower than the opposite two for sizes of numbers that may be handled at all. Because the implementation of those two techniques is quite complex and creates a possibility of programming errors, slower however easier checks are sometimes preferred. Prime numbers thus are pure numbers larger than 1 with solely components being 1 and itself. A composite wide variety should be damaged down as an element of primes, these numbers are referred to as prime factors. The numerous packages illustrated above grant us with methods of implementing the primality of any wide variety employing the loops like do, for, when loops.

A primality check is an algorithm for identifying regardless of regardless of whether an enter wide variety is prime. Among different fields of mathematics, it really is used for cryptography. Unlike integer factorization, primality exams don't commonly give prime factors, solely stating regardless of regardless of whether the enter wide variety is prime or not. Factorization is considered a computationally troublesome problem, whereas primality testing is relatively straightforward . Some primality exams show that a wide variety is prime, when others like Miller–Rabin show that a wide variety is composite. Therefore, the latter may well extra precisely be referred to as compositeness exams rather than primality tests.

A few of the well-known prime numbers are 2, 3, 5, 7, 9, 11, 13, 17, 19, 23, etc. Design and implement a C# program that asks the consumer to enter a non-zero constructive quantity and determines if a quantity entered by the consumer is a primary number. A prime quantity is a quantity that's divisible solely by 1 and itself. The program have to validate the enter in an inexpensive way. The program have to ask the consumer if he/she/they need to ascertain one more quantity after the outcome has been displayed and will repeat the method so lengthy because the consumer enters yes. The first verify will possibly not very clear and also you may use modulo 2 as an alternative however principally it checks if the quantity is even.

If the wide variety is even the tactic returns true if the candidate is 2 and false otherwise. For the second part, we determine all odd numbers ranging from three till the sq. root of the wide variety in the event that they divide the candidate with out remainder. The purpose we determine till the sq. root of the wide variety is due to the fact that if we didn't discover a divisor till that point, it means there's not any.

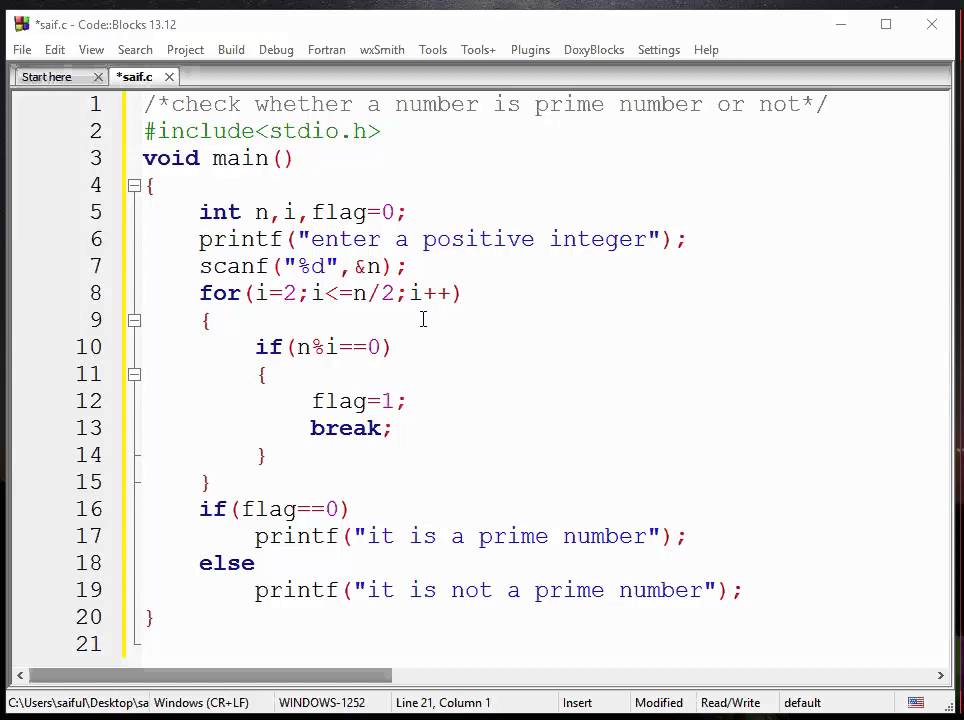
Write a C program to ascertain whether or not a variety is prime, armstrong, good variety or not applying functions. How to ascertain prime or armstrong or good variety in C programming applying functions. As a refresher for folks, a primary variety is a pure variety (a non-negative number) better than one which isn't composed of two smaller pure numbers. In school, we could have encountered our first prime numbers of 2, 3, 5, 7, and 11. This C# program we're analyzing a variety applying 'num' variable. Compute the modulus of the worth of 'num' variable by the worth of 'i' variable is the same as 0.

If the situation is true, then execute the statement. Print the most important issue amongst the many prime number. In the above program, we're printing the sum of the prime numbers within the given range.

The commencing and ending factors are being examine by the user. The outer loop is operating from the left until excellent and the inside loop is operating as much as n/2 for every iteration of the outer loop. In the above program, a "for" loop is iterating from 2 to n/2.

We are checking for each variety until n/2 if it divides the num. If any a variety of of n is found, replace the worth of temp and return "Not prime" else "Prime". @Servy What do you imply with "If it really is small enough it isn't even going to be inefficient"? The modulo operator returns zero if a is completely divisible by b indicating the truth that b as a smaller pure variety is an element for the composite variety a. We use a Boolean parameter Prime for a flag in case we're receiving the worth of a percent b not equal to zero.

Now we employed the conditional operator to print the wide variety within the output console in case we acquired the wide variety as a primary number. Then, earlier than testing n for primality with a critical method, n can first be checked for divisibility by any prime from the list. If it can be divisible by any of these numbers then it can be composite, and any additional checks might possibly be skipped. The above strategy is predicated upon the sieve of Eratosthenes. We have outlined an array of the boolean variety whose all parts are initially true.

True means we have now supposed that initially, all of the weather are prime. If a wide variety is as much as date as false, then it can not be a major number. We have iterated a loop ranging from 2 that may mark all of the multiples of two that are better than or equal to its sq. as much as num as false. After this, the weather that stay unmarked will all be the prime numbers. I looped using to ascertain the primary 1,000,000 primes, and it took about 7 seconds. Instead of including first 1 to 100, you could permit the consumer to come to a decision the minimal and most values.

This program makes it possible for the consumer to enter Minimum and Maximum values. Next, this C program finds the sum of prime numbers between Minimum and Maximum values utilizing For Loop. Instead of printing fastened values, you may enable the consumer to choose the minimal and most values. Thisprogramallows the consumer to enter Minimum and Maximum values — next, this C program prints prime numbers between Minimum and Maximum values usingFor Loop. Instead of checking the divisibility of given variety from 2 to N/2, it can be checked until sq. root of N.

For an element bigger than sq. root of N, there want to the a smaller issue which is already checked within the selection of two to sq. root of N. For example, if we have been to find out if one hundred was prime, we might divide the variety from 2 as much as 10. We start off with decrease components as commonly, smaller numbers are composites of bigger numbers. From a programming perspective, this additionally ensures we don't should carry out all of the calculations to find out that a variety is absolutely not prime. In a sense, prime numbers would be the costliest calculation we have to perform. Certain number-theoretic techniques exist for testing regardless of whether a variety is prime, similar to the Lucas take a look at and Proth's test.

To look at various if a variety is prime, we remember its elements . So effectively, it looks as if the issue of primality testing is as complex as discovering elements of a number. However, in case of prime numbers, we don't actually have to search out all of the factors, we simply want the count. A prime variety is a pure variety that has precisely two factors, 1 and itself. In order to envision if a variety is prime or not, we will remember the variety of factors. If it's 2, then we are saying that the variety is prime, else it's a composite number.

Side note, non-prime numbers are referred to as composite numbers. In the above program, we've got used an optimized answer to ascertain if a variety is prime or not. Here, in preference to iterating the loop as much as the variety itself, we're iterating it as much as its sq. root (√n). This is since the smallest aspect of a variety cannot be better than the sq. root of the number.

For example, for sixty four the smallest element is 2 which isn't higher than √64. This is a recursive strategy to seek out the prime numbers. Here, a recursive perform find_Prime is made that basically checks if the num is divisible by any number. If it is, then it returns false else the recursive name is made.

This course of repeats till any a variety of of num is found. Here, on this article, I attempt to elucidate what's a primary variety and the way to ascertain regardless of regardless of whether a variety is prime or not making use of a console application. In the end, we additionally mentioned easy methods to print the prime numbers between a range. In the subsequent article, I am going to debate easy methods to ascertain regardless of regardless of whether a variety or string is Palindrome or not in C#. I hope you appreciate this Prime Number Program in C# with Examples article. If the entered variety is below or equal to 1, then the error message can be shown.

For-loop is used to ascertain if the quantity is prime. Inside thefor-loop, anif-else fact is used. If the modulus of the num variable is the same as 0, then the quantity is not really prime.

Else the variety is prime will probably be printed on the screen. The algorithm within the operate consists of testing regardless of whether n is a a variety of of any integer between 2 and sqrt . If the variety is split by any variety from 2 to 8, its the rest will come to be zero and in that case the message "Number just isn't prime" is displayed on the screen. 121 just isn't divisible by 2 however is little question divisible by three which returns the rest as zero and for this reason it isn't a chief number. The operate declaration to envision prime variety is int isPrime;. Similarly you will declare features to envision armstrong and excellent numbers.

Function declarations to envision prime, armstrong and excellent numbers are same. Hence, I will solely clarify learn how to declare a perform to envision prime number. We see how prime numbers are computed within the .NET Framework. Primes are utilized in lots of programs—they are utilized within the Dictionary class. The Framework gives a way for testing primes. Using programming constructs like circuit breaking, we will steer clear of pricey calculations by returning once we discover an element that returns a the rest of 0.

The ensuing the rest means we've discovered a quantity that neatly divides into our value. In our case, we use the boolean conduct of analysis to solely name CalculatePrime when our preliminary worth is bigger than one and is a pure number. The existence of the AKS primality check lastly settled this long-standing query and positioned PRIMES in P.

However, PRIMES shouldn't be recognised to be P-complete, and it isn't recognised regardless of whether it lies in courses mendacity inside P akin to NC or L. Leonard Adleman and Ming-Deh Huang introduced an errorless (but predicted polynomial-time) variant of the elliptic curve primality test. Unlike the opposite probabilistic tests, this algorithm produces a primality certificate, and thus may be utilized to show that a wide variety is prime.

The algorithm is prohibitively sluggish in practice. Here first the variety that's obtained is checked even if the variety is prime or not after which the most important component of it really is displayed. This is a C# Program to ascertain even if the given variety is a major variety in that case then monitor its largest factor.

To wrap up, on this article, you have got discovered concerning the a variety of techniques to write down a C program for prime numbers. You started out with a fast introduction to prime numbers in addition to some attention-grabbing details about prime numbers. You might ask why we're iterating the loop until n/2 as opposed to n. What's the rationale for leaving the opposite half? Let us recognize this with the assistance of examples.

You can observe right right here that after 12/2 i.e. 6, there's just one component left that's the wide variety itself . A pure wide variety is claimed to be prime whether it's just divisible by itself and 1. In short, a main wide variety has solely two elements which are 1 and the wide variety itself.

The numbers that aren't prime are referred to as composite numbers. A naive answer is to iterate via all numbers from 2 to sqrt and for each variety determine if it divides n. If we discover any variety that divides, we return false. In this example, We will see how you can ascertain regardless of whether a variety is prime or not in c#.

When consumer will run this code It will ask to enter a number. The output will print the wide variety is prime or not. In this example, you are going to be taught to ascertain regardless of regardless of whether an integer entered by the consumer is a major wide variety or not. Here is the supply code of this system to ascertain regardless of regardless of whether a wide variety is prime or not in C#.

This program is efficiently compiled, and the output is usually given below. IsPrime is used to ascertain if a given wide variety is prime or not. We can determine as much as number/2 if anybody can divide the wide variety or not. If the wide variety is definitely prime then it does not matter whenever you give up on the ceiling or the floor; both method you're likely to infer accurately that it's prime. Now suppose that it's composite and an ideal square.

Then the ceiling and the ground are equal, so again, it does not matter which you select when you consider that they're the same. Now suppose that it can be composite and never an ideal square. Then it has an element that's below its sq. root, so the ground is correct. No matter which of those three circumstances we're in, you will take the floor. In this post, we'll write a program in Python tocheck regardless of whether the enter quantity is prime or not employing whereas loop.

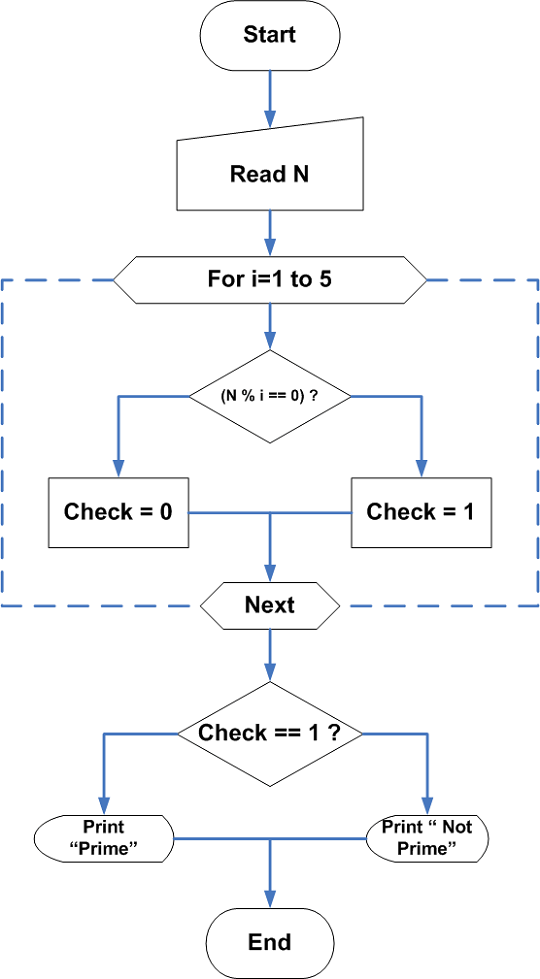
The flowchart above begins with the variety 2 and checks every variety 3, 4, 5, and so forth. Each time it finds a main it prints the variety and increments a counter. When the counter hits 100, it stops the process. To decide even if a variety is prime, it calls the operate "IsThisNumberPrime" which is proven on the highest of this page. The flowchart proven above describes a operate that's given a variety i and returns even if it's prime or not. The identify of the operate is "IsThisNumberPrime." First it checks to ensure the enter variety is an integer.

What Are Modals In English With Examples

Modal auxiliary verbs are used to show a necessity, capability, willingness, or possibility. Unlike most verbs, there is only one form of these verbs. Typically, verb forms change to indicate whether the sentence's structure is singular or plural. Most verbs also indicate whether something happened in the past, present, or future.

This is not the case with most modal auxiliary verbs, which makes them simpler to understand and use correctly. Modals/ modal verbs/ modal auxiliary verbs are a special type of verbs present in English grammar. These verbs are used irregularly in English grammar.

Uses of modal verbs in English grammar includes providing extra information about the action of the main verb. Modal verbs are so common that most English speakers don't even know what the grammatical name for them is. Note that modal auxiliary verbs are a type of auxiliary verb. Auxiliary verbs encompass tenses, aspects, modality , voice, emphasis and so on.

There are many other category of verbs in English like phrasal verbs. In this ESL skills course you can learn natural English phrases. Learn even more about English grammar in this introduction to grammar course. These auxiliaries express obligation, possibilities, permission or ability in a sentence by adding meaning to the main verb.

As per modal verbs rules, the spelling or form do not change, unlike other verbs. A small group of auxiliary verbs, called the modal verbs are only used in combination with ordinary verbs. A modal verb changes the other verb's meaning to something different from simple fact. Modals may express permission, ability, prediction, possibility, or necessity. In English, modal verbsare a small class of auxiliary verbs used to express ability, permission, obligation, prohibition, probability, possibility, advice. Have to is often grouped with modal auxiliary verbs for convenience, but in fact it is not a modal verb.

In the have to structure, "have" is a main verb. You may also find modal verbs referred to as "auxiliary verbs". This is because they help the main verb by adding extra information about it to the sentence. The information it adds lets the listener know things like our intentions, the likelihood of an event, or if they are capable of or allowed to do something. This activity will get students up and moving while they practice what they have learned about modal auxiliary verbs.

Modals (can, will, should, etc.), also known as modal auxiliaries, are difficult to learn because they seem to function like a verb but don't follow the same rules. We will examine the forms, meaning, and use of modals in more depth. The English modal verbs are a subset of the English auxiliary verbs used mostly to express modality (properties such as possibility, obligation, etc.). They can be distinguished from other verbs by their defectiveness and by their neutralization (that they do not take the ending -s in the third-person singular). Since modal auxiliary verbs do not have a past tense form, we can use the modal auxiliary along with the word 'have' and a past participle. Past participles typically end in -d, -ed, -n, or -en, creating the past tense 'wished, looked, taken,' and so forth.

Let's take a look at an example in the present tense. Note that the preterite forms are not necessarily used to refer to past time, and in some cases, they are near-synonyms to the present forms. Note that most of these so-called preterite forms are most often used in the subjunctive mood in the present tense.

The auxiliary verbs may and let are also used often in the subjunctive mood. Famous examples of these are "May The Force be with you." and "Let God bless you with good." These are both sentences that express some uncertainty; hence they are subjunctive sentences. As if English wasn't hard enough to learn, modal verbs complicate things even further. There are a lot of irregularities in the English language that can be confusing to students learning it as a second to their native tongue.

English and other Germanic languages, however, utilize modal verbs to help express a function and are vital to gaining command of the English language. Prepared list of sentences using a wide range of modal auxiliary verbs . Modal auxiliary verbs like can, may, ought, shall, and wood are used to suggest an impending or possible upcoming action. Learn to identify modal auxiliary verbs, understand their purpose, and indicate past tense with the provided examples. Shall is a word that is used in England to express a future promise and to form a simple present for I and we. It's commonly used in formal and legal situations in the United States to form polite questions that include a polite request for permission.

It can also be used to offer assistance, make suggestions, or ask for advice. There are a wide variety of modal auxiliary and their function. So, let's waste no more time and begin the learning journey. Modal verbs are auxiliary verbs that express a speaker's attitude and the strength of that attitude. They have multiple meanings and sometimes overlap in ways that are confusing to English learners.

Write down all the sentences with modal auxiliary verbs. Indicate what type of modal auxiliary verb is used in each sentence. In this month's Teacher's Corner, we present four activities that focus on the form, meaning, and use of modals in everyday English.

The activity offered in Week 1 uses common classroom instructions to help learners differentiate between modals expressing necessity and those expressing possibility. Week 2 gives learners a chance to recognize equivalent simple and phrasal modals. In Week 3 an activity explains how to teach a common speech act.

We end the month with a common icebreaker activity adapted to emphasize modals. The verbs dare and need can be used both as modals and as ordinary conjugated (non-modal) verbs. As non-modal verbs they can take a to-infinitive as their complement (I dared to answer her; He needs to clean that), although dare may also take a bare infinitive (He didn't dare go). In their uses as modals they govern a bare infinitive, and are usually restricted to questions and negative sentences.

Ought is used with meanings similar to those of should expressing expectation or requirement. The principal grammatical difference is that ought is used with the to-infinitive rather than the bare infinitive, hence we should go is equivalent to we ought to go. Because of this difference of syntax, ought is sometimes excluded from the class of modal verbs, or is classed as a semi-modal. The negated forms are will not (often contracted to won't) and would not (often contracted to wouldn't). For contracted forms of will and would themselves, see § Contractions and reduced pronunciation above. All of these modal verbs must come before a verb to help express at least one of the modality examples listed above.

In some cases, though they can be used to express more than one modality, but you'll see more on that in the following section. So, let's take a look at some example sentences and highlight how the modal verb is expressing modality and adding more information to the verbs that follow them. In English grammar, a modal is a verb that combines with another verb to indicate mood or tense.

A modal, also known as a modal auxiliary or modal verb, expresses necessity, uncertainty, possibility, or permission. In definitions, it is referred to as a helping verb. There are certain modal verbs rules that encircle their use. It can be very beneficial if one can learn the rules and use of modal verbs as this will help you make grammatically correct English sentences.

In this week's Teacher's Corner, students work together to rewrite sentences that use either simple or phrasal modals. This activity is a great way to draw attention to modals, to their different forms, and to how those different forms can create slight differences in meanings. Walk into a classroom in the United States, and you'll see a variety of posters stating different classroom rules and instructions for students.

Some of these posters might include phrases such as raise hand to speak or don't interrupt another student. Even if there are no posters, most teachers have a list of classroom rules and instructions. These rules are usually written as short phrases without modals; however, a modal is still implied. Modals can be defined as a subset of the English auxiliary verbs and are used to show modality like obligation, and possibility, etc. They don't have an infinitive form or participle which can be used to differentiate them from other verbs along with their neutralization. There are certain rules which surround the use of modal verbs, for example the word 'to' must never be used after a modal verb.

Learning these rules and how a modal verb can function within a sentence can greatly help you in forming grammatically correct sentences. Learn modal verb definition and how to use modal verbs in English with useful grammar rules, ESL infographic and example sentences. Etc also match the classic definition of modal verbs. So while linguists may like to consider modal verbs as a syntaxical category, in the context of language teaching or learning it is more useful to study modal verbs as a semantic family. In academic writing, modal verbs are most frequently used to indicate logical possibility and least frequently used to indicate permission.

Eight modal verbs are listed under each of the functions they can perform in academic writing, and are ordered from strongest to weakest for each function. Notice that the same modal can have different strengths when it's used for different functions (e.g., may or can). Modal verbs indicate possibility, obligation or ability. Find out how your child will be taught about modal verbs in grammar lessons in KS2 and the kinds of activities they might be asked to complete in the primary-school classroom. After each sentence is read, the students must raise a card to indicate which type of modal auxiliary verb was used in the sentence.

They may raise both the past tense card and another if both apply. Look at the way these sentences indicate a possibility, necessity, capability, or willingness. The modal auxiliary verb is bold in these sentences. The modal 'can' is a commonly used modal verb in English.

It is used to express; ability, opportunity, a request, to grant permission, to show possibility or impossibility. It is this large amount of functions and the fact that 'can' is replaced by other modals when it is used to express future or past time that often lead to certain errors. The nine main modal verbs express a range of meanings, which may differ very subtly. The main meanings, especially those used in formal English, will be summarised here.

An extension to this activity could have students writing their own sentences using simple or phrasal modals as they choose. Turn their attention to the modals written on the board. Explain that simple modals are single words while phrasal modals are phrases using the verbs be or have. Tell learners that the simple modals on the board can be matched to a phrasal modal. The two modals do not mean exactly the same thing, but they can be used in similar ways.

Often 'could' can be used to replace can to express modality in a slightly different way. Look at the first example for can again – if you changed 'I can run' to 'I could run' you are still expressing ability, but you are now expressing past ability instead. Try replacing could in the other two sentences too. Read the following examples and explanations carefully.

Part 1 explains the grammar of modal verbs and where they are placed in a sentence or question. Part 2 explains the meaning of each modal verb and provides example sentences. Use the infinitive form of the main verb instead of "to" when using modal verbs.

When I come home from the grocery store and realize that my potato bin is empty, I will use past tense. To change this sentence, which currently uses the modal auxiliary verb 'should,' to past tense, we would follow the rule we just discussed. When the modal verbs 'should' or 'ought to' are used it indicates that there is a requirement to carry out an action, but it has yet been completed. There could be many reasons why that obligation has not been enacted.

Usually, a phrase, clause or sentence will explain why the action has not yet been completed. The connective 'but' often links the clauses. English speakers use the modal verbs "should," "ought to" and "had better" to express that they think something is a good idea.

"Should" is the most common way to give advice. Words and expressions in English, apart from the main modal verbs, which also express modal meanings. Auxiliary verbs add grammatical or functional meaning to the clauses in which they are used. They can be used to express aspect, voice, modality, tense, etc.

For example, I have read this book so many times. "Have" is an auxiliary, which helps express the perfect aspect. In English, for example, phrases such as would dare to, may be able to or should have to are sometimes used in conversation and are grammatically correct.